Chapter 7 Solutions

Contributed by Felipe Grimaldi Avileis and Matt Nolan 2017

7.1. George’s Utility = $ln(x)$

Starting wealth = 1000000

If he wins he gets 1,000 , if he loses 1,000 .

Therefore:

$ln(1000000) = \pi(bullswin) * ln(1100000) + (1-\pi(bullswin))*ln(900000)$

$ln(1000000)= ln(900000) + \pi(bullswin)*(ln(1100000)-ln(900000))$

$\pi(bullswin) = (ln(1000000) - ln(900000))/ (ln(1100000) - ln(900000))$

Computing we get that $\pi(bullswin) = .525042$ or 52.5%, meaning that George believes the bulls have, at least, a 52.5% chance of winning the NBA finals.

7.5. Ms. Fogg’s Utility = $ln(Y)$

Prob of losing 1,000 = 25% or .25

Therefore

$E[U(Y)] = .25*ln(9,000) + .75*ln(10,000)$

$E[U(Y)] = 9.184$

In order to prove to her that her utility would be greater after she purchase’s the insurance, all we need is to compare the utility’s with and without insurance.

From a) we know that $E[U(Y)] = 9.184$

So we calculate U(Y) with the fair actuarial rate of $250.

$U(Y) = ln(10000-250) = 9.185$

As $U(Y)> E[U(Y)]$ we can prove to her that it is better to buy insurance at this rate.

Max insurance, form definition, is the difference between Initial Wealth and CE. As shown below:

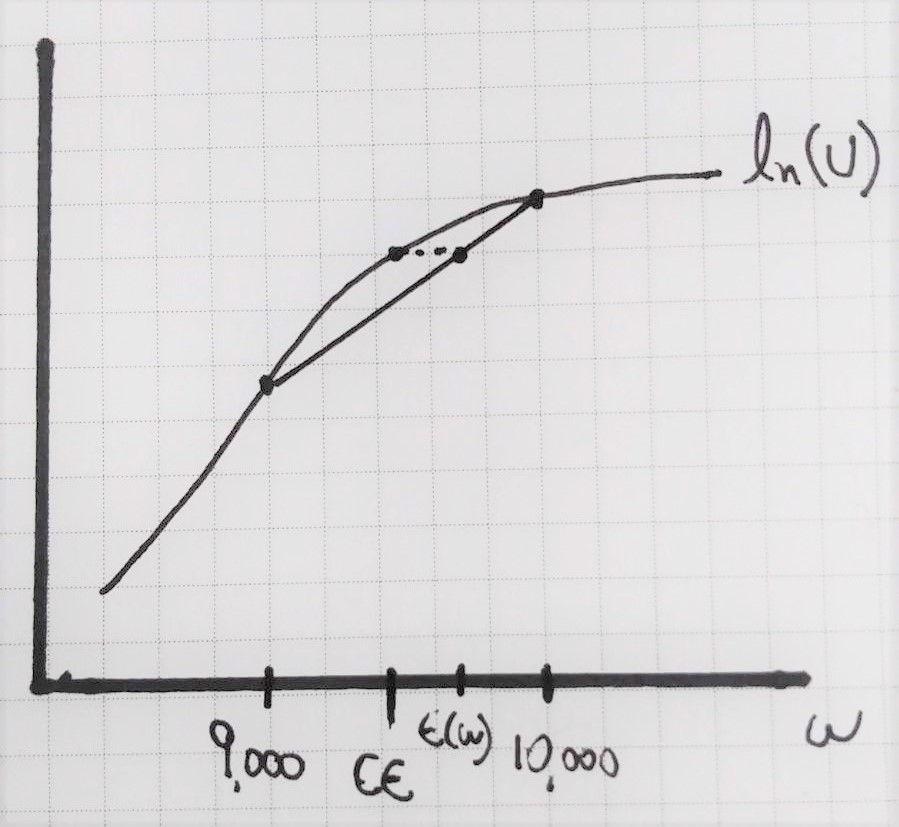
Figure 1.

If we know Initial Wealth is 10,000, we only need to find CE.

$U(CE) = E[U(gamble)]$

$ln(CE) = 9.184$ (from a)

$CE = 9,740.04$

Using Initial Wealth - CE = max premium, we get

$Max Prem = 10,000 - 9,740.04$

$Max Prem = 259.97$

7.7

A farmer believes there is a 50–50 chance that the next growing season will be abnormally rainy. His expected utility function has the form

expected value = $\frac{1}{2}\ln\Upsilon_{NR} + \frac{1}{2}\ln\Upsilon_{R}$

where $\Upsilon_{NR}$ and $\Upsilon_{NR}$ represent the farmer’s income in the states of “normal rain” and “rainy,” respectively.

Suppose the farmer must choose between two crops that promise the following income prospects:

Crop	$\Upsilon_{NR}$	$\Upsilon_{R}$
Wheat	28,000	10,000
Corn	19,000	15,000

Which of the crops will he plant?

$EV(Wheat) = \frac{1}{2}28,000 + \frac{1}{2}10,000 = 19,000$ $EV(Corn) = \frac{1}{2}19,000 + \frac{1}{2}15,000 = 17,000$

$EU(Wheat) = \frac{1}{2}\ln28,000 + \frac{1}{2}\ln10,000 = 9.725$ $EU(Corn) = \frac{1}{2}\ln19,000 + \frac{1}{2}\ln15,000 = 9.734$

Here, the farmer produces both corn and wheat even though the expected value for wheat exceeds the expected value for corn. This is because the farmer’s utility of wealth is concave. In other words, this individual is risk averse and chooses to plant at least some corn because corn profits less susceptible to the risks posed by abnormally high levels of rain.

Suppose the farmer can plant half his field with each crop. Would he choose to do so? Explain your result.

$EU(\frac{1}{2}Wheat,\frac{1}{2}Corn) = \frac{1}{2}\ln19000 + \frac{1}{2}\ln17,000 = 9.74912$

Because the farmer’s expected utility for planting half of his field with wheat and half of his field with corn exceeds the expected utility of planting any one crop exclusively, he may consider this strategy as an option. However as we see in in the next step, the farmer maximizes his expected utility by planting these crops in a more optimal proportion.

What mix of wheat and corn would provide maximum expected utility to this farmer?

\[\begin{align*} EU(\alpha, 1 - \alpha) &= \frac{1}{2}\ln[\alpha28,000 + (1- \alpha)19,000]+\frac{1}{2}\ln[\alpha10,000 + (1- \alpha)15,000] \\ EU(\alpha, 1 - \alpha) &= \frac{1}{2}\ln[19,000 + 9,000\alpha]+\frac{1}{2}\ln[15,000 - 5,000\alpha] \end{align*}\]

Then, to find optimal proportion, we take the partial derivative with respect to $\alpha$.

\[\frac{\partial EU}{\partial \alpha}= \frac{1}{2}\frac{9,000}{19,000 + 9,000\alpha}+\frac{1}{2}\frac{-5,000}{15,000 - 5,000\alpha}=0\]

Solving the first order condition, we find $\alpha = .4\overline{4}$ and $(1-\alpha) = .5\overline{5}$.

In these proportions, the farmer’s expected utility is:

\[\begin{align*} EU &= \frac{1}{2}\ln[(.4\overline{4})28,000 + (.5\overline{5})19,000]+\frac{1}{2}\ln[(.4\overline{4})10,000 + (.5\overline{5})15,000] \\ EU &= 9.74935 \end{align*}\]

So, if the farmer wishes to optimize his expected utilility he should devote approximately 44% of his field to wheat production and 56% to corn production.

Would wheat crop insurance—which is available to farmers who grow only wheat and which costs 4,000 and pays off 8,000 in the event of a rainy growing season—cause this farmer to change what he plants?

\[EU(Wheat+Insurance) = \frac{1}{2}\ln(28,000-4000) + \frac{1}{2}\ln(10,000-4,000+8,000)\]

\[EU(Wheat+Insurance) = 9.8163\]

In this scenario, the farmer is better off if he purchases the insurance and only grows wheat.