Chapter 12 Solutions
Contributed by Conner Naughton and Gowthami Venkateswaran 2017
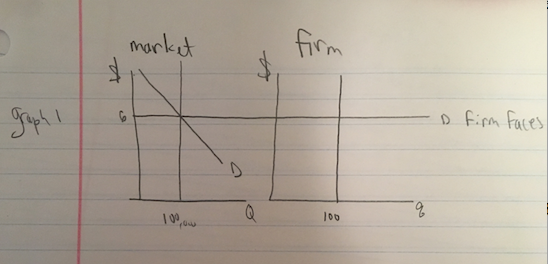
12.3 a) \(n = 1000\), \(q = 100\)
fixed supply
\[Q = 100*1000 = 100,000\]
equilibrium: \[supply = demand\]
\[100,000 = 160,000 - 10,000p\]
\[10,000p = 60,000\]
\[p = \$6\]
\[Q = 100,000\] \[ n = 1000\]
- Graphs: 1
- Graphs: 2
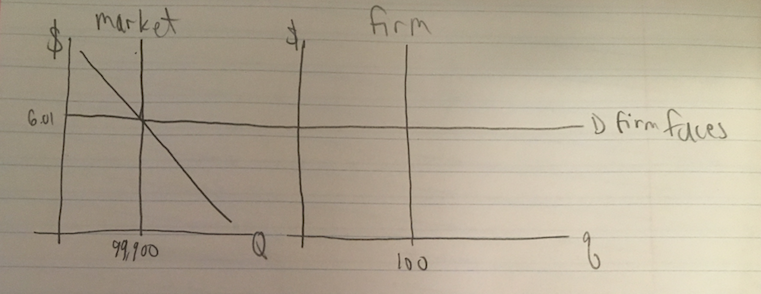
\[99,900 = 160,000 - 10,000P\]
\[P = 6.01 \]
If one firm sells nothing, other firm faced with demand: \(P = 6.01\)
Graph 3
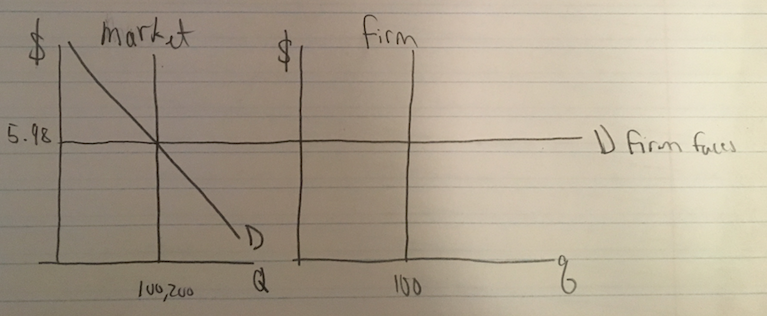
\[100,200 = 160,000 - 10,000P \]
\[P = 5.98\]
If one firm instead sells 200.
- Industry demand elasticity.
Demand elasticity faced by an individual firm. Perfectly elastic (market is perfectly competitive).
12.5)
Demand: \(Q = 1500 - 50P\)
\[C(q) = \frac{1}{2}q^2 - 10q +w\]
\[\begin{align*} MC(q) &= q-10 \\ p &= q-10 \\ q &= p+10 \end{align*}\]\[AC(q) = \frac{q}{2}-10 + \frac{w}{q}\] Market supply can be expressed by:
\[Q= n*q = n(p+10)\]
So the market clearing condition is:
\[S=D\]
\[\begin{align*} n(p+10) &= 1500-50p \\ np+n*10 &=1500-50p \\ (50+n)p &=1500-10n \\ \end{align*}\]Subbing in the entreprenuer condition \(n=0.25w\)
\[\begin{align*} (50+\frac{w}{4})P &=1500-\frac{10w}{4} \end{align*}\]Now, from the no profit condition we know that the MC equals to the Average cost.
\[q-10=\frac{q}{2}-10+\frac{w}{q}\]
\[\frac{q}{2}=\frac{w}{q}\] \[q^2=2w\] \[q=\sqrt{2w}\] Then subbing this into the \(q=p+10\) equation,
\[w = \frac{(p+10)^2}{2}\] Now we have found two equations with only \(p\) and \(w\) in it. Two equations in two unknowns should be possible to solve.
\[[50 + \frac{(p+10)^2}{8}]p = 1500 - 10\frac{(p+10)^2}{2} \] Verify that \(P=10\) solves this equation. Then it follows that \(q=20\), \(n=50\), \(Q=1000\).
12.6)
\[STC = \frac{q^2}{2}+10q+5\]
\[SMC = q+ 10\] a) Firm
\[ p=SMC\]
\[p=q + 10 inverse supply\]
\[q =p-10 supply\]
Industry: 100 firms =>
\[Q=100(P-10) supply\]
b)Demand:
\[Q=1100-SOP\]
D=S =>
\[1100-SOP=100P-1000\]
\[2100 = 150P\]
\[$14=P^*\]
\[Q^*=1100-SO.14 = 400\]
\[q=4\]
Firm’s profit - p.q - STC(q)
\[ =14(4) - (4\frac{2}{2}+10(4)+8)\]
\[=56-53\]
\[\pi firm = $3\]
- Figure 1 here
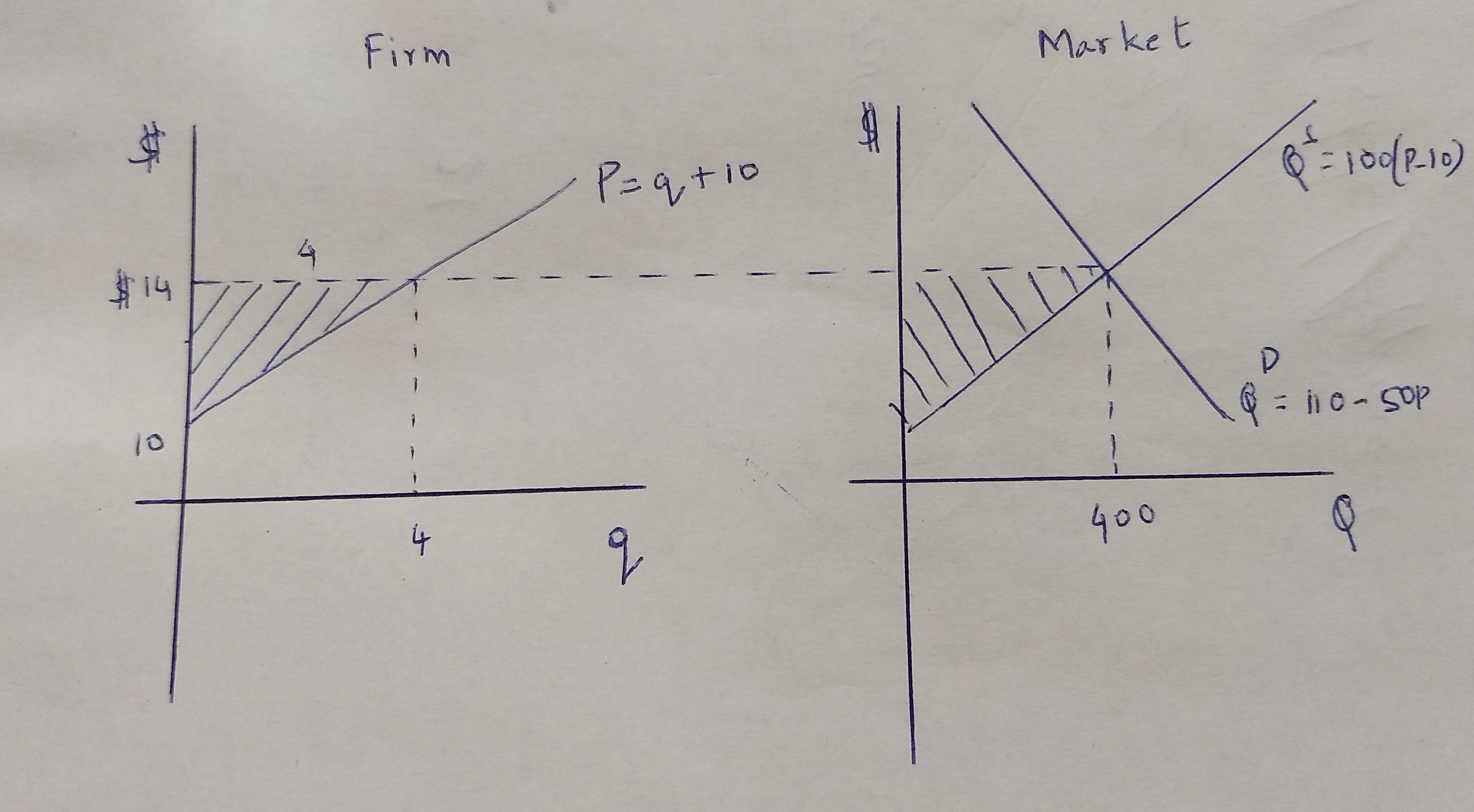
PS of 1 firm is \(\frac{1}{2}.4.4 = 8\) and there are 100 firms Total PS = \[100.8 = $800\]
- Industry Profit \[= 100.3 = $300\]
Short run fixed cost \[= 5.100 = $500 \](5 from the non-variable part of the cost function)
Industry Profit + SFC \[= 300 + 500 = 800 \](Same as total PS)
- Now SMC - q +13
\[p = q+13\]
\[q-p-13\] and\[ Q=100(p-13)\]
Clear market S=D
\[100(p-13)=1100-SOP\]
\[100p-1300=1100-SOP\]
\[150P=2400\]
\[P=$16\]
\[q=16-13-3\]
\[Q=100.3=300\]
- Figure 2 here
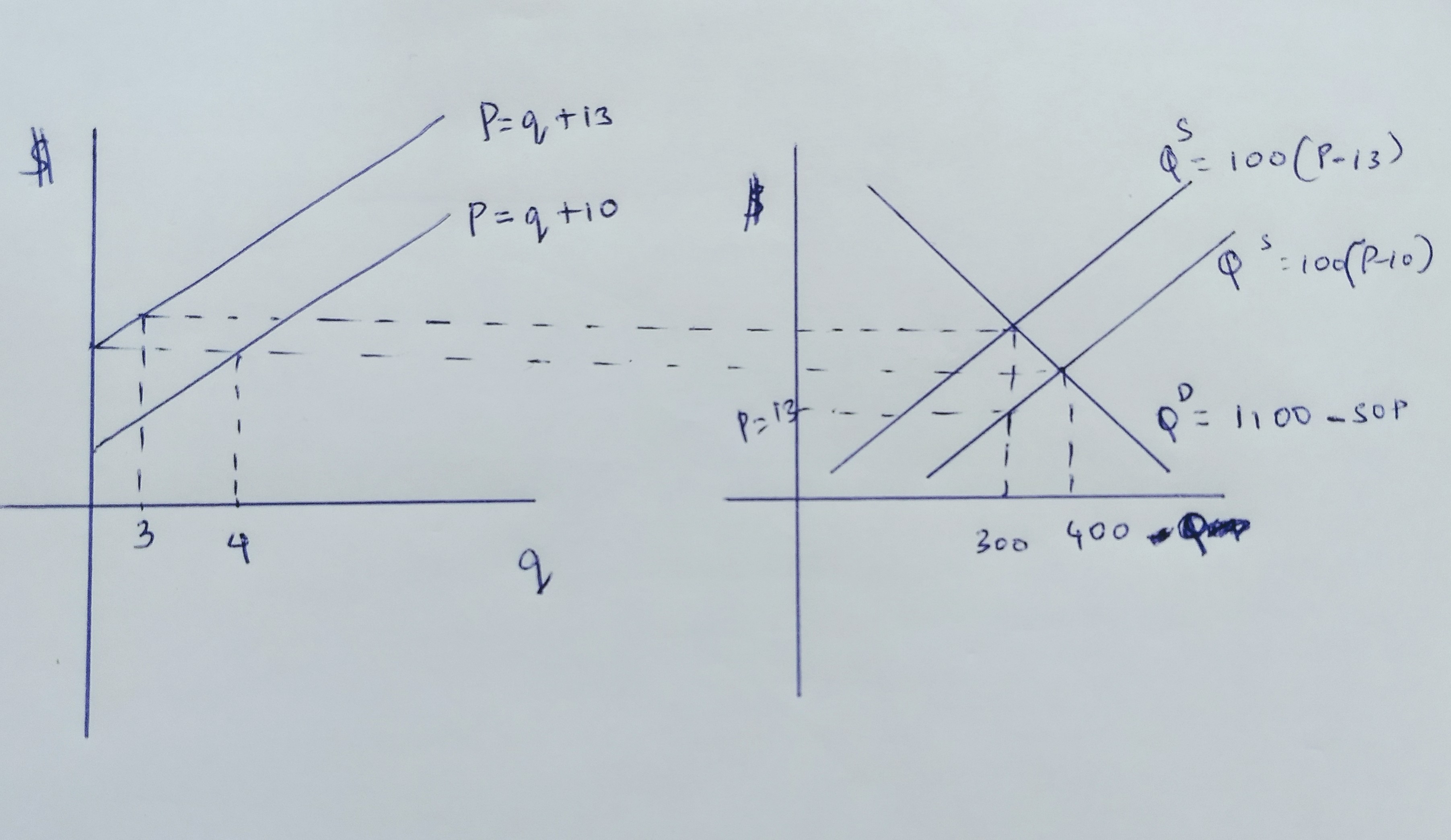
So incidence is shared $1 by producer and $2 by consumers.
\[Q = 100(P-10)\]
\[300=100(P-10)\]
\[3=P-10\] \[13=P\]
- Figure 3 here
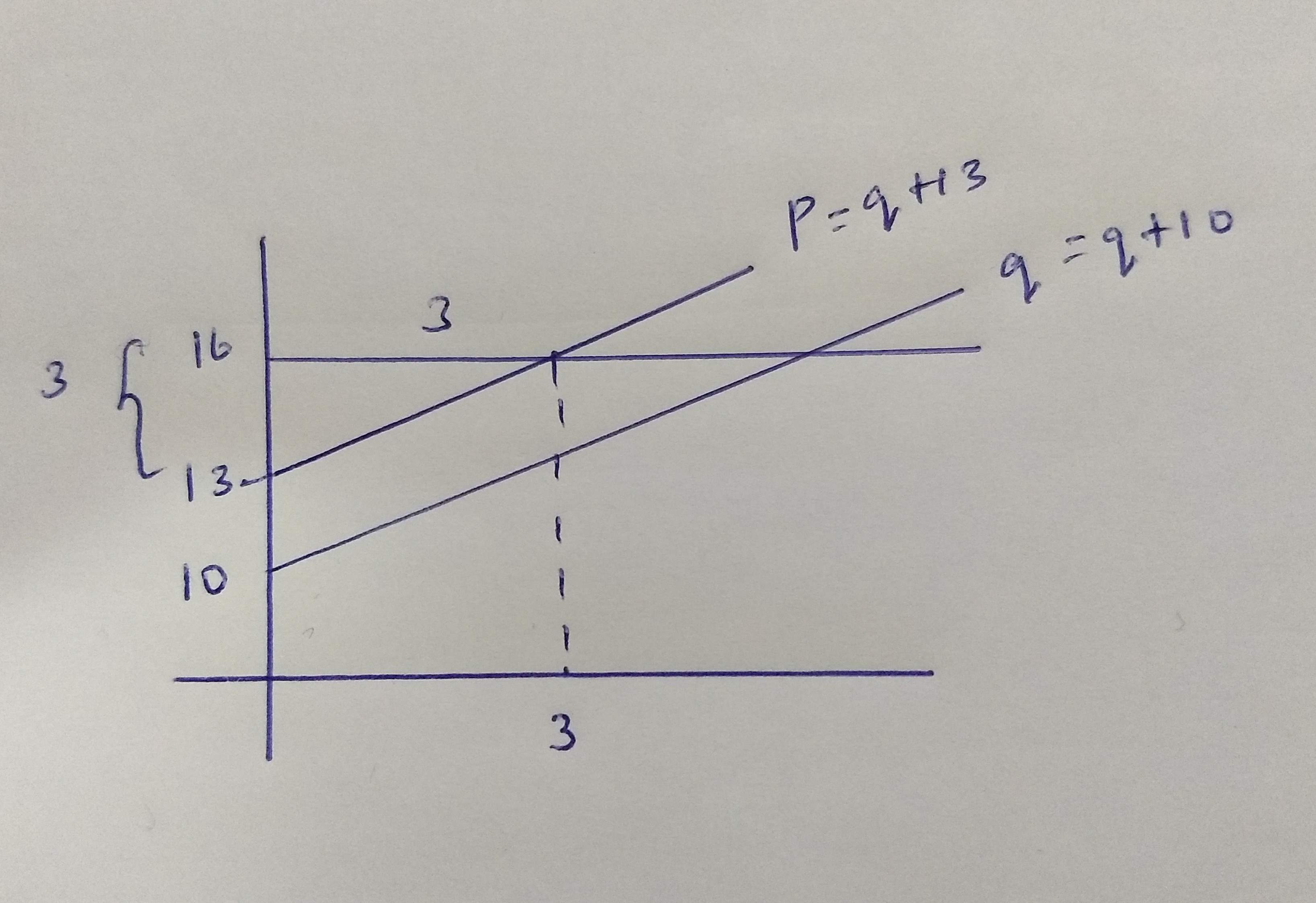
New PS =\[\frac{1}{2}3.3\]
\[ = 9/2\]
Total industry PS \[ = 100.\frac{9}{2}\]
\[ =$450\] That makes a loss in PS of \[800 - 450 = $350\]
New short and profit
\[ = 16.3 - ( \frac{3^2}{2} + 13.3 + 8)\]
\[=48-48.5\] \[= -0.50\] per firm or $-50 industry. This makes a change in profit of \[$300+$50 = $350\] decrease, same as the reduction in total PS. Only MC makes for quality decisions, the tax affects MC not FC