Chapter 11 Solutions

Contributed by Luke Gasparich and Steve Burak 2017

11.1)** (a) Maximum Profit:

$\pi(q) = 20q - .1q^2 - 10q - 50$ $\pi'(q) = 20 - .2q - 10 = 0$ $.2q = 10$ $q = 50$

(b) Maximum Daily Profit:

$\pi(50) = 20(50) - .1(50)^2 - 10(50) - 50 = 200$

(c) Graph the Results:

$S = MC = .2q + 10$

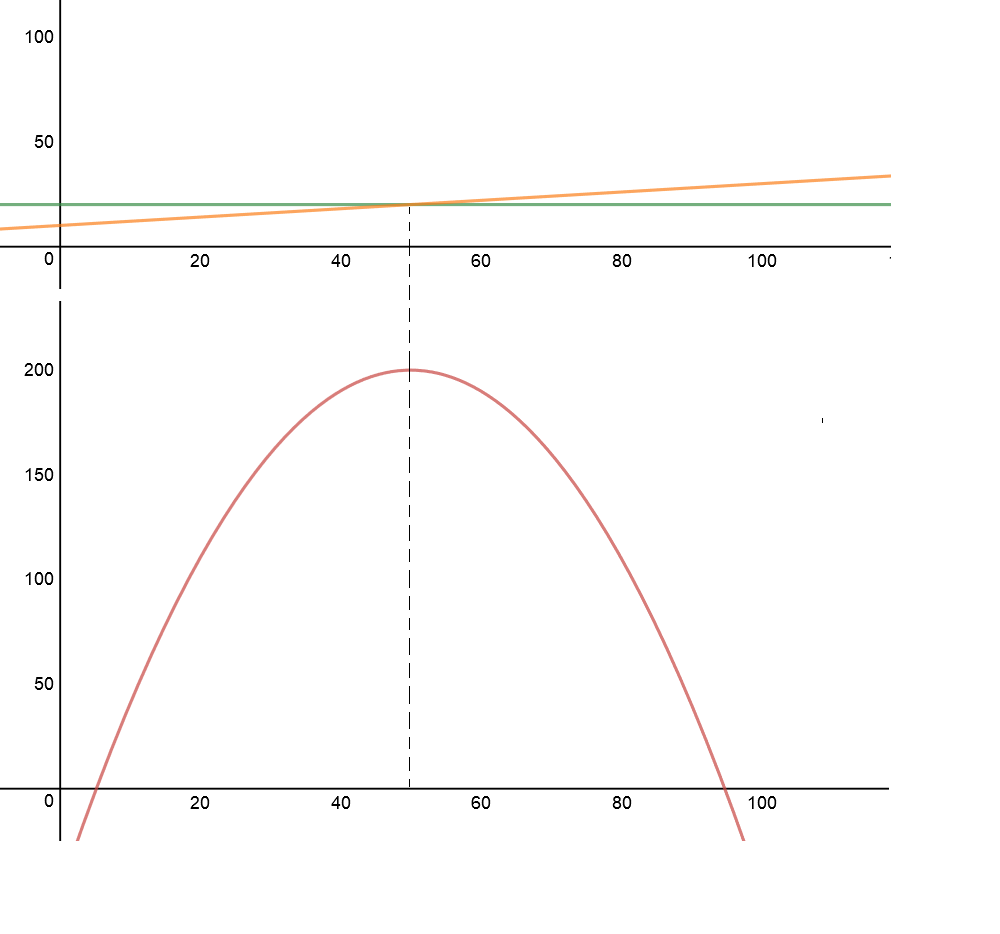
Figure 1

11.2) A lump sum tax on profits would look like this: $\pi(q) = pq - c(q) - t$ FOC: $p - c'(q) = 0$ The same as FOC without tax.

A proportional tax on profits would look like this: $\pi(q) = (1-t)[pq - c(q)]$ because the firm has to pay $t*\pi(q)$ in taxes. FOC: $(1-t)(p-c'(q)) = 0$ $=>$ $p - c'(q) = 0$ (Divide through by (1-t)) Same as above, so proportional tax on profit has no affect on output decisions.

Per unit output: $\pi(q) = pq - c(q) - tq$ FOC: $p - c'(q) - t = 0$, this one is different so per unit tax affects output choice.

11.4)

\[\pi (q)=\Big[-\frac{1}{2}q_A +50\Big]q_A +\Big[-\frac{1}{4}q_L+25\Big]q_L -0.25(q_A +q_L)^2\] $A:$ $(1):$ $-q_A+50-0.5(q_A+q_L)=0$ $(2):$$-\frac{1}{2}q_L+25-0.5(q_A+q_L)=0$

from $(1)$ \[-\frac{3}{2}q_A-\frac{1}{2}q_L+50=0\] \[-3q_A+100=q_L\] plug into $(2)$ $=>-q_L-\frac{1}{2}q_A+25=0$ \[-(-3q_A+100)-\frac{1}{2}q_A+25=0\] \[\frac{5}{2}q_A=75\] \[q_A=\frac{150}{5}\] \[q_A=30\] \[q_L=-3(30)+100)=10\] \[P_A=-\frac{1}{2}*30+50=$35\] \[P_L=-\frac{1}{4}(10)+25=$22.50\]

$11.6) a)$ \[ E[ \pi (q)] = 0.5[30q - 0.5q^2 -5q-100] + 0.5[20q - 0.5q^2 - 5q -100]\] \[=15q- \frac{1}{4}q^2- \frac{5}{2}q-50+10q- \frac{1}{4}q^2 - \frac{5}{2}q -50\] \[=- \frac{1}{2}q^2 +20q -100\] \[ \frac{dE( \pi (q))}{dq} = -q+20=0\] \[ q=20\] $c)$ \[EU[ \pi (q)]=0.5\sqrt{30q-\frac{1}{2}q^2 -5q-100} +0.5\sqrt{20q-\frac{1}{2}q^2-5q-100}\] \[\frac{dEU[\pi (q)]}{dq}=\Big(30q-\frac{1}{2}q^2-5q-100\Big)^\frac{-1}{2}(30-q-5)+\Big(20q-\frac{1}{2}q^2-5q-100\Big)^\frac{-1}{2}(20-q-5)=0\] \[\frac{25-q}{\sqrt{25q-\frac{1}{2}q^2-100}}+\frac{15-q}{\sqrt{15q-\frac{1}{2}q^2-100}}=0\] Solve this equation for higher $EU$ then if $q=20$ from part $(a)$ $q=16.95$ maximizes $EU$

$b)$ \[EU(\pi (20))=0.5\sqrt{30*20-\frac{1}{2}(20)^2-5*20-100}+0.5\sqrt{20*20-\frac{1}{2}(20)^2-5*20-100}\] \[=0.5\sqrt{600-200-100-100}+0.5\sqrt{400-200-100-100}\] \[=0.5\sqrt{200}+0.5\sqrt{0}\] \[=0.5*10\sqrt{2}\] \[=5\sqrt{2}\] \[=7.07\] $d)$ If they know with certainty that $p=30$: \[E(\pi (q))=\pi(q|p=30)\] \[=30q-\frac{1}{2}q^2-5q-100\] \[\pi '(q)=30-q-5=0\] \[q=25\] If they know $p=20$ \[\pi (q)=20q-\frac{1}{2}q^2-5q-100\] \[\pi '(q)=20-q-5=0\] \[q=15\]